Answer:
C.

Step-by-step explanation:
Given the below function;
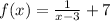
To find the inverse of the above function, we have to follow the below steps;
1. Replace f(x) with y;
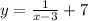
2. Switch x and y;

3. Solve for y;
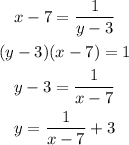
4. Replace y with f^-1 (x);

To find the domain of the function, we need to consider that value of x that will make the function undefined and exclude it. That value of x is 7. So x must not be equal to 7.
Therefore, the solution is as written below;
