2 Answers

Sk Saad Al Mahmud · Answer 1 · 2023-04-06T11:40:42+0000

The vector is given to be:

For a vector v given to be:

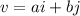
the trigonometric form is given to be:

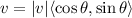
$v=|v|\langle\cos \theta,\sin \theta\rangle$

where

$|v|=\sqrt[]{a^2+b^2}$

and

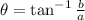
$\theta=\tan ^(-1)(b)/(a)$

Comparing this to our vector, we have:

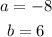
$\begin{gathered} a=-8 \\ b=6 \end{gathered}$

Therefore,

$\begin{gathered} |t|=\sqrt[]{(-8)^2+6^2}=\sqrt[]{64+36}=\sqrt[]{100} \\ |t|=10 \end{gathered}$

and

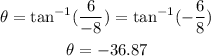
$\begin{gathered} \theta=\tan ^(-1)((6)/(-8))=_{}\tan ^(-1)(-(6)/(8))_{} \\ \theta=-36.87 \end{gathered}$

Since the angle is negative, we can add 180° to the angle to get the positive angle. Therefore:

$\theta=-36.87+180=143.13$

Therefore, the vector in trigonometric form will be:

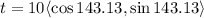
$t=10\langle\cos 143.13,\sin 143.13\rangle$

The correct option is the SECOND OPTION.

Please log in or register to add a comment.