Question

Find the volume of the tunnel created inside the block.

Answer 1

In the given figure, the tunnel is in the shape of a cylinder.

The diameter of the tunnel, D=4 ft

Hence, the radius of the tunnel is,

`r=(D)/(2)=(4)/(2)=2\text{ ft}`

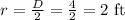
The height of the cubical block, a=6 ft.

The height of the tunnel is the same as the height of the cubical block.

Hence, the height of the tunnel, h=a=6 ft.

Now, the volume of the tunnel in the shape of a cylinder can be calculated as,

`\begin{gathered} V=\pi r^2h \\ =\pi*2^2*6 \\ =75.4ft^2 \end{gathered}`

Therefore, the volume of the tunnel created inside the block is 75.4 sq.ft.