Question

There are a total of 256 people at a party. If, after every 5 minutes, half of the people present leave , how many people present leave, how many people will still remain after 20 minutes？

Answer 1

The total amount of people is 256.

You know that every 5 minutes, half of the people leave the party. To determine how many people leave for every time period, you can determine an exponential equation.

Let "x" represent the time periods, and every time period will be 5 minutes

"y" represents the number of people after "x" time periods

"a" represents the initial value

"1-r" represents the decay factor. Where "r" is the decay rate, in this case, 0.50

The exponential equation can be constructed as follows:

`\begin{gathered} y=a(1-r)^x \\ y=256(1-0.5)^x \\ y=256\cdot0.5^x \end{gathered}`

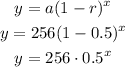
You need to know how many people will be at the party after 20 minutes, first, divide 20 by 5 to calculate how many time periods have passed after 20 minutes

`x=(20)/(5)=4`

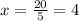
Replace the equation with x=4

`\begin{gathered} y=256\cdot0.5^4 \\ y=256\cdot0.0625 \\ y=16 \end{gathered}`

After 20 minutes there will be 16 left in the party.