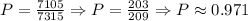A)
We will solve using:
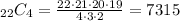
The number of ways to choose 4 girls from 12 girls and 0 boys from 10 boys is:
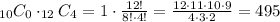
So, the probability() of choosing 4 just 4 girls is:

So, that is the probability to get just 4 girls on the committee.
B)
For the committee to be just 4 boys is found as follows:
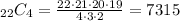
And the number of ways to choose 4 boys from 10 boys and 0 girls from 12 girls is:
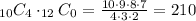
So, the probability to get just 4 boys on the committee is:

C)
For the committee to have at least one girl is:
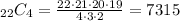
No. of ways to selecting at least 1 girl:
22C4 - 10C4 = 7315 - 210 = 7105
Now, we calculate the probability: