Question

14 1/2, 12 3/4, 11, ________, _______, ________, ________, 2 1/4 1/2

Answer 1

`14(1)/(2),\text{ 12}(3)/(4),\text{ 11, }9(1)/(4),\text{ }7(1)/(2),\text{5}(3)/(4),\text{ }4,\text{ 2}(1)/(4),\text{ }(1)/(2)`

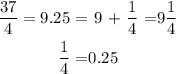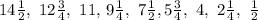
1) Examining this Sequence, we have an Arithmetic Sequence whose ratio is

r = -7/4, therefore we can fill in the gaps by adding each term to -7/4, so we have:

`\begin{gathered} 14(1)/(2),\text{ 12}(3)/(4),\text{ 11, }9(1)/(4),\text{ }7(1)/(2),\text{5}(3)/(4),\text{ }4,\text{ 2}(1)/(4),\text{ }(1)/(2) \\ 11\text{ -}(7)/(4)\text{ =}(37)/(4)\text{ or 9}(1)/(4) \\ (37)/(4)-(7)/(4)=(15)/(2)\text{ or } \\ (15)/(2)-(7)/(4)=(23)/(4)\text{ or 5}(3)/(4) \\ (23)/(4)-(7)/(4)=(16)/(4)\text{ = 4} \\ 4-(7)/(4)=(9)/(4) \end{gathered}`

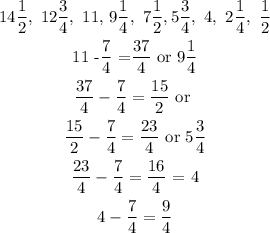
Since in an Arithmetic Sequence each term is obtained by adding or subtracting a common ratio, in this case, r= -7/4

2) To transform a mixed number into a fraction, we need to keep the denominator from the original mixed number, and write the numerator as the product of the denominator by the whole number and add to the numerator:

`\text{9}(1)/(4)=\frac{(4\text{ }*9+1)}{4}=(37)/(4)`

To turn an improper fraction into a mixed number we need to divide the numerator by the denominator and write the whole number and the fraction

`\begin{gathered} (37)/(4)=9.25\text{ = 9 + }(1)/(4)\text{ =9}(1)/(4) \\ (1)/(4)\text{ =0.25} \end{gathered}`