Given:
The altitude of a right circular cone = 15
The radius of the base = 8
A cylindrical hole of diameter 4 is drilled through the cone, with its axis along the axis of the cone.
So, the radius of the cylinder = 2
We will find the height of the cylinder using the ratio and proportional
Let the height of the cylinder = h
so,
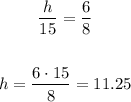
So, the height of the cylinder = 11.25
The volume of the solid = the volume of the cone - the volume of the cylinder
The volume of the cone =
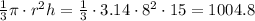
The volume of the cylinder =
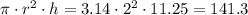
So, the volume of the solid =

so, the answer will be: Volume of the solid = 863.5