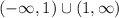Answer:
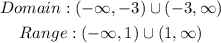
Explanation:
Given the function:
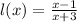
Domain
The domain of a function is the set of the values of x at which the function is defined.
A rational function is undefined when its denominator equals 0.
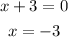
Therefore, the domain of l(x) is:
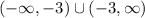
Range
The range of a function is the set of the values of L(x) at which the function is defined.
Since L(x) is a rational function, find the horizontal asymptote.
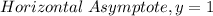
Therefore, the range of the function is: