Question

Consider an object moving through water (density of 1000 kg/mº) versus air (density of1.29 kg/m).What is the ratio between the forces, i.e. what'sFp(water)Fplair)

Answer 1

Given data:

* The density of water is,

`d_w=1000kgm^(-1)`

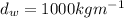
* The density of air is,

`d_a=1.29kgm^(-1)`

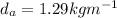
Solution:

Force in terms of density is,

`F\propto d`

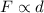
Thus, the ratio of force in water to force in air is,

`\frac{F_(\rho(water))}{F_(\rho(air))_{}}=(d_w)/(d_a)`

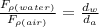
Substituting the known values,

`\begin{gathered} (F_(\rho(water)))/(F_(\rho(air)))=(1000)/(1.29) \\ (F_(\rho(water)))/(F_(\rho(air)))=775.19 \end{gathered}`

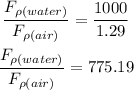
Thus, the ratio between the force at water to force at air is 775.19