Question

How to fine the rang for f(x) and the rang for the inverse functon

Answer 1

`\begin{gathered} \text{range of f(x)= (-}\infty,0)\cup(0,\infty) \\ \text{range of f(x)=x}<0\text{ or x}>0 \\ \text{rangeof f}^(-1)(x)=(-\infty,1)\cup(1,\infty) \\ \text{rangeof f}^(-1)(x)=x<1\text{ or x}>1 \end{gathered}`

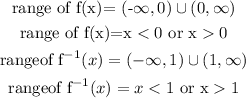
Step-by-step explanation

Step 1

find the inverse of the function

a) let

`y=(4)/(x^3-1)`

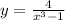
now, swap the variables and isolate

`\begin{gathered} y=(4)/(x^3-1)\leftrightarrow x=(4)/(y^3-1) \\ \end{gathered}`
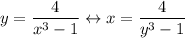
`\begin{gathered} x=(4)/(y^3-1) \\ x(y^3-1)=4 \\ y^3-1=(4)/(x) \\ y^3=(4)/(x)+1 \\ y=\sqrt[3]{(4)/(x)+1} \\ \end{gathered}`

find the DOMAIN of the inverse, this would be the range for f(x)

so

therefore, the range of f(x)

`\begin{gathered} \text{range of f(x)= (-}\infty,0)\cup(0,\infty) \\ \text{range of f(x)=x}<0\text{ or x}>0 \end{gathered}`

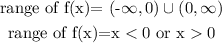
Step 2

Now, as the range of a functino is the domain of its inverse,

the range of the inverse will be the domain of f(x), hence

a) find the domain of f(x)

`y=(4)/(x^3-1)`

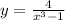
the domains is all real numbers except the number/s that make the denominator equals zero,s o

`\begin{gathered} x^3-1=0 \\ x^3=1 \\ x=1 \end{gathered}`

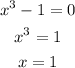
therefore, the range of the inverse function is

`\begin{gathered} \text{domain f(x)=rangeof f}^(-1)(x) \\ \text{rangeof f}^(-1)(x)=(-\infty,1)\cup(1,\infty) \\ \text{rangeof f}^(-1)(x)=x<1\text{ or x}>1 \end{gathered}`

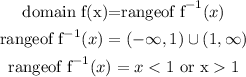
I hope this helps you