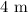Question

Please Help I'm Confused...Tessa has leaned a ladder against the side of her house. The ladder forms a 63˚ angle with the ground and rests against the house at a spot that is 8 meters high. Which length is the best approximation for the distance along the ground from the bottom of the ladder to the wall?1. 2 m2. 3 m 3. 4 m4. 5 m

Answer 1

The length that is the best approximation for the distance along the ground from the bottom of the ladder to the wall is;

`4\text{ m}`

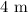
Step-by-step explanation:

Given the figure in the attached image.

The length along the ground from the bottom of the ladder to the wall is the length of line AB.

Applying trigonometry;

`\tan \theta=(opposite)/(adjacent)`

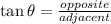
given;

`\begin{gathered} \theta=63^(\circ) \\ \text{opposite = BC = 8m} \\ \text{adjacent = AB} \end{gathered}`

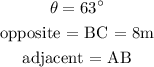
Substituting the given values;

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan 63=(8)/(AB) \\ AB=(8)/(\tan 63) \\ AB=4.076 \\ AB=4\text{ m} \end{gathered}`

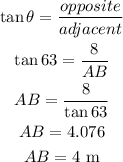
Therefore, the length that is the best approximation for the distance along the ground from the bottom of the ladder to the wall is;

`4\text{ m}`