Question

You are given the sample mean and the population standard deviation. Usethis information to construct the 90% and 95% confidence intervals for thepopulation mean. Interpret the results and compare the widths of theconfidence intervals.From a random sample of 33 business days, the mean closing price of acertain stock was $124.47. Assume the population standard deviation is$10.68.

Answer 1

Given:

• Sample size, n = 33

,

• Sample mean, x' = 124.47

,

• Standard deviation, σ = 10.68

Let's construct the 90% and 95% confidence interval.

• (a). 90% confidence interval.

For a 90% confidence interval, the level of significance, α = 1 - 0.90 = 0.10

Using the z-score table, we have:

`z_{(\alpha)/(2)}=z_{(0.10)/(2)}=z_(0.05)=1.645`

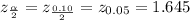
Now, let's find the margin of error, E:

`\begin{gathered} E=z_{(\alpha)/(2)}*\frac{\sigma}{\sqrt[]{n}} \\ \\ E=1.645*\frac{10.68}{\sqrt[]{33}} \\ \\ E=3.058 \end{gathered}`

To find the 90% confidence interval, apply the formula:

`\begin{gathered} C.I=x^(\prime)\pm E \\ \\ CI=124.47\pm3.058 \\ \\ C\mathrm{}I=124.47-3.058,\text{ 124.47 + 3.058} \\ \\ C\mathrm{}I=121.41,\text{ }127.53 \end{gathered}`

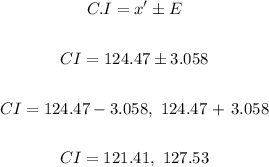
The 90% confidence interval is ( 121.41, 127.53)

• (,b). ,The 95% confidence interval

The level of significance: 1 - 0.95 = 0.05

Find the z-score using the z-score table:

`z_{(\alpha)/(2)}=z_{(0.05)/(2)}=z_(0.025)=1.96`

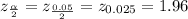
Now, find the margin of error:

`\begin{gathered} E=z_{(\alpha)/(2)}*\frac{\sigma}{\sqrt[]{n}} \\ \\ E=1.96*\frac{10.68}{\sqrt[]{33}} \\ \\ E=3.644 \end{gathered}`

To find the 95% confidence interval, we have:

`\begin{gathered} CI=x^(\prime)\pm E \\ \\ CI=124.47\pm3.644 \\ \\ CI=124.47-3.644,\text{ 124.47+3.644} \\ \\ CI=120.83,\text{ 128.11} \end{gathered}`

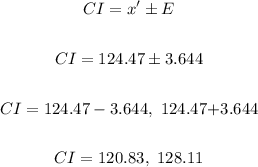
The 95% confidence interval is 120.83, 128.11

ANSWER:

90% confidence interval is ( 121.41, 127.53)

95% confidence interval is (120.83, 128.11)