Part A. Write and solve an equation that can be used to find the value of y.
Given: (Using the principles of vertical angles.)
Solution:
Equation: 2(-2 + y) = 20
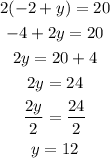
Part B. Write and solve an equation that can be used to find the value of x.
Given: (Using the sum of the angles of a straight line.)
Note: The sum of the angles of a straight line is equal to 180 degrees.
Solution:
Equation: 5x + 36 + 20 = 180

ANSWERS:
Part A: 2(-2 +y) = 20, y = 12
Part B: 5x + 36 + 20 = 180, x = 24.8