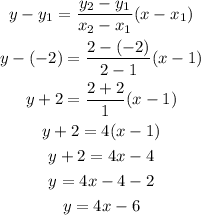Question

What is (1, -2) and (2, 2) as a linear equation

Answer 1

We have to find the equation of the line going through the two pair of points given.

The equation is:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

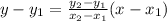
The 2 pair of points are:

`\begin{gathered} (x_1,y_1)=(1,-2) \\ \text{and} \\ (x_2,y_2)=(2,2) \end{gathered}`

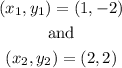
Now, we just subtitute the coordinates (points) into the respective variables in the equation and do some algebra to get the equation of the line. Shown below:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-(-2)=(2-(-2))/(2-1)(x-1) \\ y+2=(2+2)/(1)(x-1) \\ y+2=4(x-1) \\ y+2=4x-4 \\ y=4x-4-2 \\ y=4x-6 \end{gathered}`