Question

- Save & Exit Certify Lesson: 3.3 Measures of Relative PositionVANESSA DENISE CISNEROSQuestion 2 of 12, Step 1 of 11/15CorrectThree potential employees took an aptitude test. Each person took a different version of the test. The scores are reported below.Kaitlyn got a score of 78.2; this version has a mean of 73.8 and a standard deviation of 11.Rebecca got a score of 256.3; this version has a mean of 236 and a standard deviation of 29.Tera got a score of 7.24; this version has a mean of 6.7 and a standard deviation of 0.9.If the company has only one position to fill and prefers to fill it with the applicant who performed best on the aptitude test, which of the applicants should be offered thejob?TablesAnswerKeypadKeyboard ShortcutO KaitlynO Rebecca

Answer 1

Given -

Kaitlyn Score = 78.2

Kaitlyn Mean = 73.8

Standard deviation = 11

Rebecca score = 256.3

Rebecca mean = 236

Standard deviation = 29

Tera score = 7.24

Tera mean = 6.7

Standard deviation = 0.9

To Find -

Which of the applicants should be offered the job =?

Step-by-Step Explanation :

We know, the formula for z-score:

`\begin{gathered} z-score\text{ = }\frac{x\text{ - }\mu}{\sigma} \\ \\ Where,\text{ x = Score} \\ \mu\text{ = Mean} \\ \sigma\text{ = Standard Deviation} \\ \\ \end{gathered}`

z-score of kaitlyn =

`\begin{gathered} z-score\text{ = }(78.2-73.8)/(11) \\ \\ z-score\text{ = }(4.4)/(11)\text{ = 0.4} \end{gathered}`

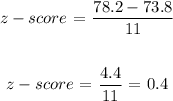
z-score of Rebecca =

`\begin{gathered} z-score\text{ = }(256.3-236)/(29) \\ \\ z-score\text{ = }(20.3)/(29)\text{ = 0.7} \end{gathered}`

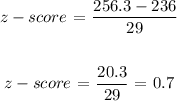
z-score of Tera =

`\begin{gathered} z-score\text{ = }(7.24-6.7)/(0.9) \\ \\ z-score\text{ = }(0.54)/(0.9)\text{ = 0.6} \\ \\ \end{gathered}`

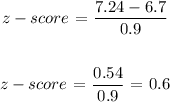
Now,

The applicant with the highest z-score is most likely to be offered the job.

Rebecca has the highest z-score of 0.7

Final Answer -

Rebecca should be offered the job.