Question

Write(27a^-9)^-2/3wiein simplest form.

Answer 1

We are asked to write in its simplest form the expression :

`(27a^(-9))^{(-(2)/(3))}`

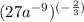
So we start by writing the most external power (-2/3) in root form. Recall that a denominator in the exponent's fraction is the index of the radical that has to be used. on the other hand, the numerator of the exponents fraction is a power. Also recall that when there is a NEGATIVE sign in the exponents such implies that the algebraic expression to which it is applied flips to its RECIPROCAL.

Then starting with the negative in the a^-9 we get:

`((27)/(a^9))^{(-(2)/(3))}`

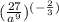
and now using the negative sign in the external exponents, we get the reciprocal of the fractional expression as shown below:

`((27)/(a^9))^{(-(2)/(3))}=((a^9)/(27))^{((2)/(3))}`

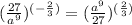
Now we apply the radical form we discussed before:

`((a^9)/(27))^{((2)/(3))}=(\sqrt[3]{((a^9)/(27)})^{})^2`

Now we use the fact that a^9 and 27 are perfect cubes, in order to cancel the cubic root:

`\sqrt[3]{((a^9)/(27)})=\frac{\sqrt[3]{a^(3\cdot3)}}{\sqrt[3]{3^3}}=(a^3)/(3)`

and finally, raise this expression to the power 2 :

`((a^3)/(3))^2=(a^6)/(9)`

Therefore a^6/9 is the simplest form of the algebraic expression that was given