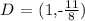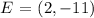Solution:
Let the function:
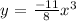
Since it is a cubic function, its graph is
now, the points on the graph, that are requested are obtained as follows:
For x= 0 then
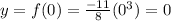
thus, the point with x equals zero is:
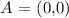
now, for x = -1 then:
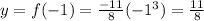
thus, a point with a negative x value is:
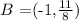
also, for x = -2, we get:
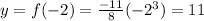
then, another point with a negative x value is:
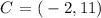
now, if x = 1, then
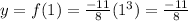
thus, a point with a positive x value is:
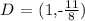
also, if x = 2, we get:
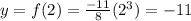
then, another point with a positive x value is:
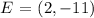
On the graph, these points are:
So that, we can conclude that the correct answer is:
The graph of the function is:
one point with x equals zero is:
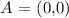
two points with negative x values are:
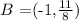
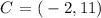
two points with positive x values are: