Solution:
Let the missing length (hypotenuse) be represented by x
To find the value of x, we will apply the Pythagorean theorem formula which is

Where the radius, r of the circle is
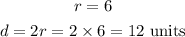
Where
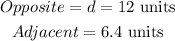
Substitute the values of the opposite and adjacent into the Pythagorean theorem above
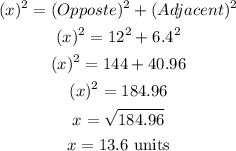
Hence, the answer is 13.6 units