Question

dfigle measures of a triangle given angles with variablesIn the triangle below, suppose that m ZV=(x +4)", mW = (x+4)", and m 2 X = (4x - 2)°.xFind the degree measure of each angle in the triangle.(x+4).(x + 4)+m Z V =m ZW =Х(4x - 2)mZx =.

Answer 1

Given:

• m∠V = (x + 4)°

,

• m∠W = (x + 4)°

,

• m∠X = (4x - 2)°

Let's find the measure if each angle.

To find the measure of each angle, apply the Triangle Angle Sum theorem which states that the sum of interior angles in a triangle is 180 degrees.

Thus, we have:

m∠V + m∠W + m∠X = 180

(x + 4) + (x + 4) + (4x - 2) = 180

• Solve for x:

x + 4 + x + 4 + 4x - 2 = 180

• Combine like terms:

x + x + 4x + 4 + 4 - 2 = 180

6x + 6 = 180

• Subtract 6 from both sides:

6x + 6 - 6 = 180 - 6

6x = 174

• Divide both sides by 6:

`\begin{gathered} (6x)/(6)=(174)/(6) \\ \\ x=29 \end{gathered}`

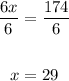
Now, substitute 29 for x in each given angle to find the measure of the angle.

• m∠V = x + 4 = 29 + 4 = 33,°

• m∠W = x + 4 = 29 + 4 = 33,°

• m∠X = 4x - 2 = 4(29) - 2 = 116 - 2 = 114,°

ANSWER:

• m∠V = 33,°

,

• m∠W = 33,°

,

• m∠X = 114,°