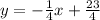Given the points (-1,6) and (3,5).
The formula to find the slope is
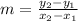
Take
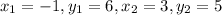
Plug the values into the formula and find the slope.
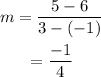
The slope-intercept form is y = mx+b.
Plug the value of m.
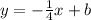
ThusConsider the point (-1,6). Substitute -1 for x and for y into the equation.
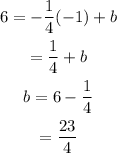
Thus, the equation of the line in slope intercept form is