Question

Use the Angle Addition Postulate and the given information bto complete each statement.

Answer 1

Let's make a diagram of the problem

Based on the given information, we can deduct that angle AFC is formed by angles AFB and BFC.

`m\angle AFC=m\angle AFB+m\angle BFC=61+44=105`

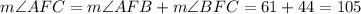
Angle AFC measures 105°.

Now, we use the supplementary angles theorem to find angle AFE.

`\begin{gathered} m\angle AFE+m\angle AFB+m\angle BFC=180 \\ m\angle AFE+61+44=180 \\ m\angle AFE=180-44-61=75 \end{gathered}`

Hence, angle AFE measures 75°.

As you can observe in the diagram, angles EFD and BFC are vertical angles, so they are equal.

Hence, angle EFD measures 44°.