Question

-ks XO Solve for x. Round your answer to the nearest 2 d T + 20 Y ard A 16 4 endar

Answer 1

In the given figure :

Angle A = 16 degrees

Length AB = 20

AC = x, BC = y

Apply the trignometric ratio of sin 16

Trignometric ratio of sine is epxress as :

`\text{ }\sin \theta=(Perpendicular)/(Hypotenuse)`

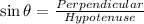
for angle =16, substitute the value of perpendicular BC =y, AB = 20

`\begin{gathered} \text{ }\sin \theta=(Perpendicular)/(Hypotenuse) \\ \sin 16=(BC)/(AB) \\ \sin 16=(y)/(20) \\ y=20\text{ }\sin 16 \\ y=20(0.275) \\ y=5.5 \end{gathered}`

Thus, we get BC = 5.5

Similarly Apply the trignometric ratio of Cosine 16

Trignometric ratio of cosine is express as:

`\cos \theta=(Base)/(Hypotenuse)`

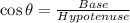
For angle = 16

`\begin{gathered} \cos \theta=(Base)/(Hypotenuse) \\ \cos 16=(AC)/(AB) \\ \cos 16=(x)/(20) \\ x=20(\text{cos}16) \\ x=20(0.961) \\ x=19.22 \end{gathered}`

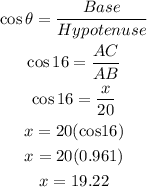
AC = 19.22

Answer : BC = 5.5, AC = 19.22