How do I solve and graph this inequality?-(x + 6) > - 2 ( 1 - x)

Question

asked Sep 1, 2023 183k views

1 Answer

Akash Verma · Answer 1 · 2023-09-06T15:25:03+0000

Solution:

The question is given below as

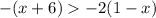
Step 1:

Expand the brackets

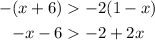
$\begin{gathered} -(x+6)>-2(1-x) \\ -x-6>-2+2x \end{gathered}$

Step 2:

Collect similar terms

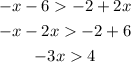
$\begin{gathered} -x-6>-2+2x \\ -x-2x>-2+6 \\ -3x>4 \end{gathered}$

Step 3:

Divide both sides by -3 (note: when divided by a negative coefficient, the inequality sign will be reversed)

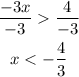
$\begin{gathered} (-3x)/(-3)>(4)/(-3) \\ x<-(4)/(3) \end{gathered}$

Hence,

The solution for the inequality is x < -4/3

The number line is given below as

While the graph is given below ( it will be graphed with a broken line)