Question

Write and equation in standard form of a circle with a center at -10 -4 and having the (4, -2) on the circle.

Answer 1

Given:

Center of circle, (h, k) = (-10, -4)

Point the circle passes through ==> (4, -2)

Let's write the equation of the circle in standard form.

Apply the standard form of a circle equation:

`(x-h)^2+(y-k)^2=r^2`

Where:

(h, k) is the radius.

r is the radius of the circle.

To find the radius, let's find the distance between the points using the distance between points:

`d=√((x_2-x_1)^2+(y_2-y_1))^2`

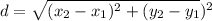
Where:

(x1, y1) ==> (-10, -4)

(x2, y2) ==> (4, -2)

Thus, we have:

`\begin{gathered} d=√((4-(-10)^2+(-2-(-4))^2) \\ \\ d=√((4+10)^2+(-2+4)^2) \\ \\ d=√(14^2+2^2) \\ \\ d=√(196+4) \\ \\ d=√(200) \\ \\ d=14.14 \end{gathered}`

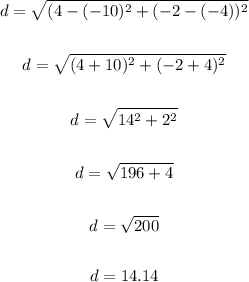
Hence, we have:

• Center, (h, k) = (-10, -4)

,

• Radius of the circle = √200

Therefore, the equation of the circle is:

`\begin{gathered} (x-(-10))^2+(y-(-4))^2=√(200^2) \\ \\ (x+10)^2+(y+4)^2=200 \end{gathered}`

ANSWER:

`(x+10)^2+(y+4)^2=200`