Question

The populations P (in thousands) of a particular county from 1971 through 2014 can be modeled byP = 71.7e0.0345twhere t represents the year, with t = 1 corresponding to 1971.(a) Use the model to complete the table. (Round your answers to the nearest whole number.)YearPopulation1980101240 Correct: Your answer is correct.1990142949 Correct: Your answer is correct.2000201843 Correct: Your answer is correct.2010285000 Correct: Your answer is correct.(b) According to the model, when will the population of the county reach 350,000

Answer 1

2016

Step-by-step explanation:

Given the populations, P (in thousands) of a particular county from 1971 through 2014 modeled by the equation;

`P=71.7e^(0.00345t)`

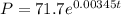
If the population of the country reached 350,000, the time it will take to reach this population can be gotten as shown below;

`\begin{gathered} 350=71.7e^(0.0345t) \\ (350)/(71.7)=e^(0.0345t) \\ 4.8815=e^(0.0345t) \end{gathered}`

Take the natural logarithm of both sides

`\begin{gathered} \ln (4.8815)=\ln e^(0.0345t) \\ \ln (4.8815)=0.0345t \\ \text{ }1.5854\text{= 0.0345t} \end{gathered}`

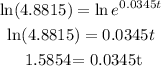
Divide both sides by 0.0345;

`\begin{gathered} (1.5854)/(0.0345)=(0.0345t)/(0.0345) \\ \text{Swap} \\ (0.0345t)/(0.0345)=(1.5854)/(0.0345) \\ t=(1.5854)/(0.0345) \\ t=45.95 \end{gathered}`

This shows that the value of t is approximately 46 according to the calculation

Since at 1971, t = 1, at t = 46, the year it will take the population of the county to reach 350,000 is 2016