Question

Pls help with this question we are using the factorial “!”

Answer 1

P(X = 1) = 0.393

Step-by-step explanation

X follows a binomial distribution, where success is "a person arrives late". The probability of success is p = 0.125 and the number of trials is n = 7,

`X\sim B(7,.125)`

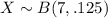
The probability that exactly x people will arrive late is,

`P(X=x)=_nC_x\cdot p^x\cdot(1-p)^(n-x)`

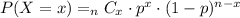
So the probability that one person arrives late is,

`P(X=1)=_7C_1\cdot0.125^1\cdot(1-0.125)^(7-1)=(7!)/(1!\cdot6!)\cdot0.125\cdot0.825^6\approx0.393`

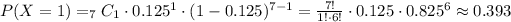
Hence, the probability that exactly one person will arrive late in a 7-person department is 0.393, rounded to the nearest thousand.