Question

Suppose that the functions p and g are defined as follows,p(x) = x² +7g(x)=√x+4Find the following,(gp) (5)=X(pog)(5) =5?

Answer 1

(gp) (5)= sqrt(32)+4

(pog)(5) = 28+8sqrt(5)

Explanation:

We are given the following functions:

`p(x)=x^2+7,g(x)=√(x)+4`

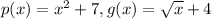
(gp) (5)=

(gp) means that the outside function is g and the inside is p:

So

`g\circ p(x)=g(x^2+7)=√(x^2+7)+4`

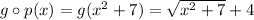
At x = 5

`(g\circ p)(5)=√(5^2+7)+4=√(32)+4`

(gp) (5)= sqrt(32)+4

(pog)(5) =

Outside p, inside g. So

`(p\circ g)(x)=p(√(x)+4)=(√(x)+4)^2+7=(√(x))^2+8√(x)+16+7=x+8√(x)+23`

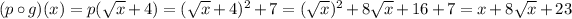
At x = 5

`(p\circ g)(5)=5+8√(5)+23=28+8√(5)`

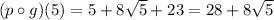
(pog)(5) = 28+8sqrt(5)