Question

Aria earned a score of 325 on Exam A that had a mean of 300 and astandard deviation of 25. She is about to take Exam B that has a meanof 51 and a standard deviation of 10. How well must Aria score onExam B in order to do equivalently well as she did on Exam A? Assumethat scores on each exam are normally distributed.

Answer 1

Since the mean of Exam A is 300 and the standard deviation is 25, Aira scored 1 standard deviation above the mean. This means

`\begin{gathered} \bar{x}+\sigma=x \\ 300+25=325 \end{gathered}`

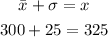
To do equivalently well in Exam B, Aira must also obtain a score of 1 standard deviation above the mean of Exam B. Thus, add the standard deviation of 10 to the mean of 51.

`\begin{gathered} \bar{x}+\sigma=x \\ 51+10=61 \end{gathered}`

Thus, she needs to have a score of 61 in Exam B.