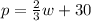Question

This graph shows how the total number of vocal pieces Will can sing depends on the numberof weeks he takes voice lessons. The variable w represents the number of weeks he hastaken voice lessons, and the variable p represents the total number of pieces he has learned.Vocal pieces will can sing10090807060Number of pieces learned504030201060708090+10010 20 30

Answer 1

The general form of a linear equation is:

`y=mx+b`

Where m is the slope, represented by:

`m=\frac{change\text{ in x}}{\text{change in y}}`

And b is the intercept with the y-axis.

We can find the slope and the intercept with the y-axis by looking at the graph we are given. We can see that in the graph the x-axis is represented with the letter w (number of weeks) and y-axis is represented with the letter p (number of pieces he has learned).

We would have a linear equation similar to this:

`p=mw+b`

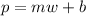
From looking at the graph, we can identify that the intercept with the p-axis is 30.

`b=30`

And to find the slope, we can take two pair of points from the line in the graph:

`m=(p_1-p_2)/(w_1-w_2)`

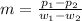
I am going to take points (30, 50) and (60,70)

`m=(50-70)/(30-60)=(2)/(3)`

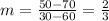
The equation for the relationship shown in the graph is:

`p=(2)/(3)w+30`