Question

A 12 N [E] force is applied to a toy train with a mass of 2.7 kg. The toy train is attached by a light string to a wagon with a mass of 1.8 kg which is attached to a second wagon with a mass of 1.0 kg. If the train is pulled on a surface with a coefficient of kinetic friction of 0.05, determine the tension in the string between the first and the second wagon. (6T, 3C) Include free body diagrams for the three masses involved in the acceleration. (3 Comm.)

Answer 1

See the attached diagram for reference and free body diagrams. The acceleration a of each body will be the same since each connecting string is in tension.

By Newton's second law, we have

• net force on the train:

- - horizontal

`\sum F = F - F_(k,T) - T_1 = m_Ta`

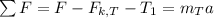
(where F = 12 N)

- - vertical

`\sum F = N_T - m_Tg = 0`

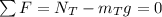
• net force on wagon 1:

- - horizontal

`\sum F = T_1 - T_2 - F_(k,1) = m_1a`

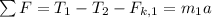
- - vertical

`\sum F = N_1 - m_1g = 0`

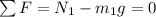
• net force on wagon 2:

- - horizontal

`\sum F = T_2 - F_(k,2) = m_2a`

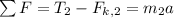
- - vertical

`\sum F = N_2 - m_2g = 0`

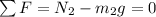
We want to determine T₂, the tension in the string connecting the two wagons.

For each body, the corresponding normal force has magnitude

N = mg

where m is the respective mass, and the kinetic friction has magnitude

Friction = 0.05 N = 0.05mg

So if µ = 0.05, then the frictional force on each body is

`F_(k,T) = 0.05 (2.7\,\mathrm{ kg}) g = 1.323\,\mathrm N`

`F_(k,1) = 0.05 (1.8\,\mathrm{ kg}) g = 0.882\,\mathrm N`

`F_(k,2) = 0.05 (1.0\,\mathrm{ kg}) g = 0.49\,\mathrm N`

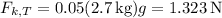
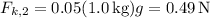
which leaves us with the system of equations,

[1] … 12 N - 1.323 N - T₁ = (2.7 kg) a

[2] … T₁ - T₂ - 0.882 N = (1.8 kg) a

[3] … T₂ - 0.49 N = (1.0 kg) a

Adding [1] and [2] eliminates T₁ :

(12 N - 1.323 N - T₁) + (T₁ - T₂ - 0.882 N) = (2.7 kg) a + (1.8 kg) a

[4] … 9.795 N - T₂ = (4.5 kg) a

Divide through both sides of [3] by 1.0 kg to solve for a :

a = (T₂ - 0.49 N) / (1.0 kg)

Substitute this into [4] and solve for T₂ :

9.795 N - T₂ = (4.5 kg) (T₂ - 0.49 N) / (1.0 kg)

(9.795 N - T₂) (1.0 kg) = (4.5 kg) (T₂ - 0.49 N)

9.795 N - T₂ = 4.5 T₂ - 2.205 N

12 N = 5.5 T₂

T₂ = (12 N) / 5.5 ≈ 2.1818 N ≈ 2.2 N