Question

4. Optimize the equation P = 3x + y using the constraints> 0,3 < 4,y> -1 andy S5.What is the maximum?03O 170-1О5

Answer 1

The equation is given to be:

`P=3x+y`

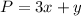
The inequalities used as a constraint for the equation are given to be:

`\begin{gathered} x\ge0 \\ x\le4 \\ y\ge-1 \\ y\le5 \end{gathered}`

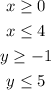
To optimize the equation, we will plot the inequalities using a graphing tool. The graph is shown below:

The white region of the graph represents the solution space.

The vertices of the graph will be used to optimize the equation. These are:

`(x,y)=(0,5),(4,5),(0,-1),(4,-1)`

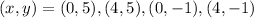
At (4, 5):

`P=3(4)+5=12+5=17`

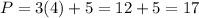
At (0, 5):

`P=3(0)+5=5`

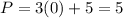
At (0, -1):

`P=-1`

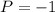
At (4, -1):

`P=11`

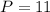
Therefore, the maximum value of P is 17.

The SECOND