Question

find the value of the ordinary annuity at the end of the indicated time period. The payment "R", frequency of deposits "m" (which is the same as the frequency of compounding), annual interest rate, "r" and time "t" are given below: Amount, $100; monthly; 3%; 4 yearsThe future value of the given annuity is $_______ (round to the nearest cent) this is the formula to use to figure this out:

Answer 1

The future value of ordinary annuity is given by the formula:

`FV=A\lbrack((1+i)^n-1)/(i)\rbrack`

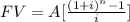
Where

A = annuity cash flow,

i = interest rate, and

n = number of payments.

The future value of annuity measures the value of the series of the recurring payments at a given point of time in future at a specified interest rate.

We are given,

A = 100

i = 0.03

n = 4 year x 12 months = 48

Substituting the values, we get:

`\begin{gathered} FV=A\lbrack((1+i)^n-1)/(i)\rbrack \\ FV=100\lbrack((1+0.03)^(48)-1)/(0.03)\rbrack \\ FV=100\lbrack((1.03)^(48)-1)/(0.03)\rbrack \\ FV\approx10440.84 \end{gathered}`Answer$10, 440.84