Question

a scientist has two solution, which she labeled solution A and solution B. each contains salt. she knowns that solution A is 60 % salt and solution B is 85% salt. she want to obtain 110 ounces of a mixture that is 75% salt. how many ounces of each solution should she use

Answer 1

The scientist has to take x ounces of the solution A and B of the solution B, so that

`x+y=110`

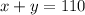
The amount of salt S this solution has is

`S=0.6x+0.85y`

Since we need a solution with 75% salt, then we need that

`\begin{gathered} (S)/(110)=0.75 \\ (0.6x+0.85y)/(110)=0.75 \\ 0.6x+0.85y=82.5 \end{gathered}`

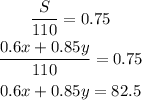
Then, we have the system of linear equations

`\begin{gathered} x+y=110 \\ 0.6x+0.85y=82.5 \end{gathered}`

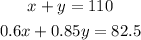
Solving for x in the first equation and replacing in the second

`\begin{gathered} x=110-y \\ 0.6(110-y)+0.85y=82.5 \\ 66-0.6y+0.85y=82.5 \\ 0.25y=16.5 \\ y=66 \\ x=110-66=44 \end{gathered}`

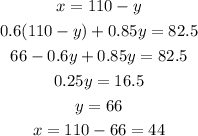
Then, if we take 44 oz of A and 66 of B we have

`0.6(44)+.85(66)=82.5`

In conclusion, the scientist needs to take 44 oz of the solution A and 66 oz of solution B.