From the diagram above,
XZ = 10 in and OX = 10 in
we are to find length of OY
XZ is a chord and line OY divides the chord into equal length
Hence, ZY=YX= 5 in
Now we solve the traingle OXY
To find OY we solve using pythagoras theorem
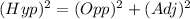
applying values from the triangle above
![\begin{gathered} OX^2=XY^2+OY^2 \\ 10^2=5^2+OY^2 \\ 100=25+OY^2 \\ OY^2\text{ = 100 -25} \\ OY^2\text{ = 75} \\ OY\text{ = }\sqrt[]{75} \\ OY\text{ = }\sqrt[]{25\text{ }*\text{ 3}} \\ OY\text{ = 5}\sqrt[]{3\text{ }}in \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1dozadgrsyn0pzfu8orz6c0zkoglbtpr7n.png)
Therefore,
Length of OY =
![5\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/fqqwcnaf0vgn1vxruh1zhjan0imgkvyyrs.png)