Question

There is one more answer it is d I will write it belowx. 2, 5, 8, 11.y -1, 0, 2, 5.

Answer 1

the table that represents a linear relatiponship is option C

Step-by-step explanation:

For the table to show linear relationship, the slope at any given two points should be equal.

slope = change iiny/change in x

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

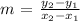
Using the first two points for the x and y values in the table:

a) slope = (5-2)/(2-1) = (8-5)/(4-2)

slope = 3/1 = 3/2

slope = 3 = 3/2

The slopes are not equal for the points used

b) slope = (5-2)/(1-(-4)) = (8-5)/(2-1)

slope = 3/(1+4) = 3/1

slope = 3/5 = 3/1

The slopes are not equal for the points used

c) slope = (5-2)/(-2-(-4)) = (8-5)/(0-(-2))

slope = 3/(-2+4) = 3/(0+2)

slope = 3/2 = 3/2

The slopes are equal for the points used

d) slope = (5-2)/(0-(-1)) = (8-5)/(2-0)

slope = 3/(0+1) = 3/2

slope = 3/1 = 3/2

The slopes are not equal for the points used

Hence, the table that represents a linear relatiponship is option C