Question

I need help on this question. This is non graded.

Answer 1

To find if the given binomials can be a difference of two squares find if both terms in the binomial have an exact square root, if both terms have a exact square root you can write if as a difference of squares:

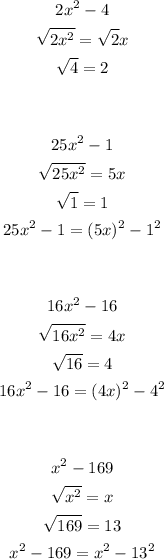
`\begin{gathered} 2x^2-4 \\ √(2x^2)=√(2)x \\ √(4)=2 \\ \\ \\ 25x^2-1 \\ √(25x^2)=5x \\ √(1)=1 \\ 25x^2-1=(5x)^2-1^2 \\ \\ \\ 16x^2-16 \\ √(16x^2)=4x \\ √(16)=4 \\ 16x^2-16=(4x)^2-4^2 \\ \\ \\ x^2-169 \\ √(x^2)=x \\ √(169)=13 \\ x^2-169=x^2-13^2 \end{gathered}`As you can see above the binomial taht cannot be written as a difference of twe squares is: 2x^2-4Answer: first option