Question

Scouting troops in Warren County are putting on a crab feed to raise money for camp. They offer a complete crab dinner as well as a vegetarian option. One troop member sold tickets for 20 crab meals and 8 vegetarian meals, with total receipts of $796. Another sold tickets for 26 crab meals and 34 vegetarian meals, bringing in a total of $1,554. How much do the two types of tickets cost?

Answer 1

Given:

a.) One troop member sold tickets for 20 crab meals and 8 vegetarian meals, with total receipts of $796.

b.) Another sold tickets for 26 crab meals and 34 vegetarian meals, bringing in a total of $1,554.

Let,

x = cost of a crab meal

y = cost of a vegetarian meal

Let's solve this using the Substitution Method.

We get,

Equation 1: One troop member sold tickets for 20 crab meals and 8 vegetarian meals, with total receipts of $796.

`\text{ 20x + 8y = 796}`

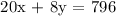
Equation 2: Another sold tickets for 26 crab meals and 34 vegetarian meals, bringing in a total of $1,554.

`\text{ 26x + 34y = 1,554}`

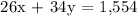
Substitute Eq. 1 to Eq. 2

20x + 8y = 796

8y = 796 - 20x

y = (796 - 20x)/8

y = 199/2 - 5x/2

26x + 34y = 1,554

26x + 6,766/2 - 170x/2 = 1,554

26x + 3,383 - 85x = 1,554

-59x = 1,554 - 3,383

-59x = -1,829

-59x/-59 = -1,829/-59

x = 31 = $31

Therefore, the crab meal costs $31.

For the vegetarian meal,

20x + 8y = 796

20(31) + 8y = 796

620 + 8y = 796

8y = 796 - 620

8y = 176

8y/8 = 176/8

y = 22 = $22

Therefore, the vegetarian meal costs $22.