Question

A restaurant has 5 side dishes, 6 main dishes and 2 desserts. A student chooses one side dish and one dessert. How many different meals could she make?

Answer 1

From the 5 side dishes, the student choose 1 side dish and can use this to make a meal in 5 ways, considering the 5 side dishes.

From the 2 desserts, she can choose 1 dessert and make meal in 2 ways, considering the 2 desserts.

In combination, we have to multiply. So the student can make meals in

`5ways*2ways=10\text{ways }`

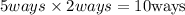
Hence the answer is 10 different meals

We can also say selecting 1 side dish from 5 side dishes and

selecting 1 dessert from 2 desserts. This becomes

`\begin{gathered} ^5C_1*^2C_1 \\ =(5!)/((5-1)!1!)*(2!)/((2-1)!1!) \\ =(5*4!)/(4!)*(2*1!)/(1!) \\ =5*2 \\ =10\text{ ways} \end{gathered}`

Hence 10 different meals