The Solution:
Given that a and b are two standard angles in the first quadrant.
We are required to find cos(a+b) if
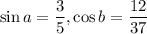
By the formula of compound angles,
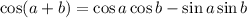
Step 1:
We need to find the value of:
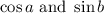
Given that:
![\begin{gathered} \sin a=(3)/(5)\text{ , and angle a is in the first quadrant, that is,} \\ 0^oBy Trigonometry we have:<p>By the Pythagorean Theorem, we can find x as below:</p>[tex]\begin{gathered} 5^2=3^2+x^2 \\ 25=9+x^2 \\ 25-9=x^2 \\ 16=x^2 \end{gathered}]()
Taking the square root of both sides, we get
![\begin{gathered} \sqrt[]{16}=\sqrt[]{x^2} \\ \pm4=x \\ x=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kprbbsuwwk1m8kvd18512b9s82vy1w4xc6.png)
So, we can get the value of:
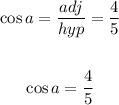
Similarly, we shall find sinb :
![\text{ If }\cos b=(12)/(37),0^o<p>By the Pythagorean Theorem, we can find y as below:</p>[tex]\begin{gathered} y^2+12^2=37^2 \\ y^2+144=1369 \\ y^2=1369-144 \\ y^2=1225 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zj1g7dtmxd9xwvx1kmqr8zsjyq6ms83zym.png)
Taking the square root of both sides, we get
![\begin{gathered} \sqrt[]{y^2}=\text{ }\sqrt[]{1225} \\ \\ y=35 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/paunm7ehxjmi3dhjoasstvizmejwajxus6.png)
So, we can get the value of:
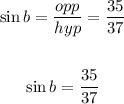
Substituting these values in the formula below:
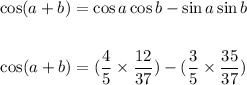
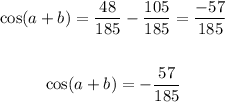
Therefore, the correct answer is [option 3]