Question

Hello I'm stuck on this problem on my homework please help

Answer 1

Given that mary deposits $93 each month in an annuity that pays 7.7% interest compounded montly.

To find the total value of the annuity in 28 years.

we have that,

The annuity formula helps in determining the values for annuity payment and annuity due based on the present value of an annuity due, effective interest rate, and several periods.

Formula for the annuity is,

`FV=P×(\left(\left(1+r\right)^n−1\right))/(r)`

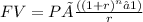
where

P is the amount, n is the time period, r is the interest rate, FV is future value.

we get that,

P=93

`r=(7.7\%)/(12)=0.641\%`

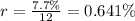
n=28x12=336

Substitute the values we get,

`FV=93*((1+(0.641)/(100))^(336)-1)/(0.00641)`

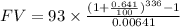
Solving this we get,

`FV=93*((1.00641)^(336)-1)/(0.00641)`

`FV=93*(8.55817-1)/(0.00641)`

`FV=93*(7.55817)/(0.00641)`
`FV=93*1179.1219`
`FV=109658.339`

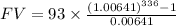
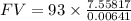
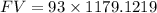
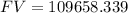
Round to nearest cent we get,

`FV=109658.34`

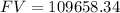
Answer is: $109658.34