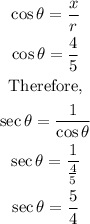Question

let θ be a reference angle such angle such that sin(θ) =-3/5 a)which quoadrants could θ be in b) if angle θ is such that sec(θ) <θ then find the values of tan(θ) and cot(θ)

Answer 1

If the reference angle is theta and, we are given;

`\sin \theta=-(3)/(5)`

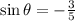
Note that sin theta is negative.

Also, we have the following on the unit circle;

`\begin{gathered} \cos \theta=(x)/(r) \\ \sin \theta=(y)/(r) \end{gathered}`

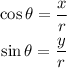
Where the value of y is negative, we would have a negative sin theta, that is;

`\sin \theta=-(y)/(r)`

This only occurs where y is negative, which is in the third and fourth quadrants. Therefore,

(a) The reference angle theta could be either in the third or fourth quadrants.

Note also that

`\sec \theta=(1)/(\cos \theta)`

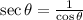
To determine the value of the cosine of this angle, we shall take the given values, y and r.

Note that r is the hypotenuse, while y is the height. To find the base x,

`\begin{gathered} r^2=x^2+y^2 \\ 5^2=x^2+3^2 \\ 25=x^2+9 \\ \text{Subtract 9 from both sides;} \\ 16=x^2 \\ \text{Take the square root of both sides;} \\ 4=x \end{gathered}`

Where the cosine is given as;

`\begin{gathered} \cos \theta=(x)/(r) \\ \cos \theta=(4)/(5) \\ \text{Therefore,} \\ \sec \theta=(1)/(\cos \theta) \\ \sec \theta=(1)/((4)/(5)) \\ \sec \theta=(5)/(4) \end{gathered}`