Question

Solve the system by substitution:2x-4y=16y=3x+11

Answer 1

Given:

The equations are 2x-4y=16 and y=3x+11.

The objective is to solve the system of equations by substitution method.

Consider the given equations as,

`\begin{gathered} 2x-4y=16\text{ ----(1)} \\ y=3x+11\text{ ----(2)} \end{gathered}`

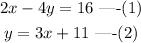
Let's take equation (1) and solve for x.

`\begin{gathered} 2x-4y=16 \\ 2x=16+4y \\ x=(16)/(2)+(4y)/(2) \\ x=8+2y----\text{ (3)} \end{gathered}`

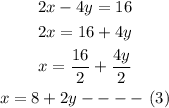
Now, substitute the value of x in equation (2) to find the value of y.

`\begin{gathered} y=3x+11 \\ y=3(8+2y)+11 \\ y=24+6y+11 \\ y-6y=24+11 \\ -5y=35 \\ y=(35)/(-5) \\ y=-7 \end{gathered}`

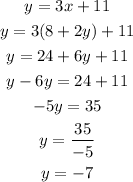
Substitute the value of y in equation (3) to find the value of x

`\begin{gathered} x=8+2y \\ x=8+2(-7) \\ x=8-14 \\ x=-6 \end{gathered}`

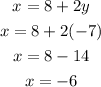
Hence, the value of x is -6 and the value of y is -7.

.