Let's use the variable x to represent Jason's speed and the variable y to represent Roger's speed.
If Jason can run 4 miles per hour faster than Roger, we can write the following equation:
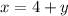
For the same time running, Jason runs 30 miles and Roger runs 18 miles, so we have:
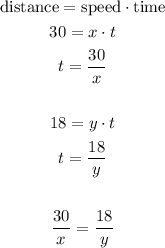
Using the value of x from the first equation, we have:

Therefore Roger's speed is 6 miles per hour.