ANSWER
3 and 7
Step-by-step explanation
If the factors are (x-3) and (x-7), we can write the polynomial as the product of its factors:

(...) is if this polynomial had more factors.
This is a product, so if any of the factors of the product is zero then the whole product is zero:
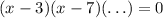
We know two of the factors, so to make the polynomial zero we have:

Therefore, two of the values that make this polynomial zero are 3 and 7.