Question

A population of wolves had 120 wolves in the year 2020 and was growing at a rate of 3% per year. (a)Write a formula for the exponential function f(t), where f(t) is the size of the wolf population t years after 2020.(b) Find the solution to the equation 60(2.1)^x=1100.

Answer 1

Given:

The initial number of wolves is a = 120.

The growth rate is r = 3%.

The objective is,

a) To write the formula for exponential function for the population of the wolf after t years.

b) To find the solution to the equation,

`60(2.1)^x=1100\text{ . . . . .. (1)}`

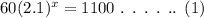
Step-by-step explanation:

a)

The general formula for the exponential growth of population is,

`y=a(1+r)^x\text{ . . . . . .(2)}`

Here, x represents the number of years which is t.

On plugging the given values in equation (2)

`\begin{gathered} f(t)=120(1+(3)/(100))^t \\ f(t)=120(1+0.03)^t \\ f(t)=120(1.03)^t \end{gathered}`

b)

The solution for given equation (1) will be,

`\begin{gathered} 60(2.1)^x=1100 \\ (2.1)^x=(1100)/(60) \\ (2.1)^x=(110)/(6) \end{gathered}`

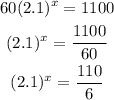
Multiply the natural logarithm on both sides of the equation,

`\begin{gathered} ln(2.1)^x=\ln ((110)/(6)) \\ x=(\ln ((110)/(6)))/(\ln (2.1)) \\ x=3.92044\ldots. \\ x\approx3.92 \end{gathered}`

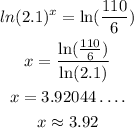
Hence,

a) The exponential function is f(t) = 120(1.03)^t.

b) The solution of the equation is 3.92.