Question

The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widgetweights have a mean of 58 ounces and a standard deviation of 9 ounces.Use the Standard Deviation Rule, also known as the Empirical Rule.Suggestion: sketch the distribution in order to answer these questions.oz anda) 99.7% of the widget weights lie betweenOZfonyb) What percentage of the widget weights lie between 40 and 85 ounces?%c) What percentage of the widget weights lie below 67 ?%Question Help: D VideoSubmit Question

Answer 1

The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all observed data will fall within three standard deviations (denoted by σ) of the mean or average (denoted by µ).

In particular, the empirical rule predicts that 68% of observations falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).

The image below shows a sketch of the distribution following the empirical rule

a) 99.7% of the widget lies between 3 standard deviations to the right and left of the mean.

`\begin{gathered} 58+3(9)=85oz_{} \\ 58-3(9)=31oz \end{gathered}`

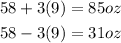
99.7% of the widget lies between 31 oz and 85 oz.

b) The percentage of the widget weights that lies between 40 and 85 ounces is calculated thus:

`49.85+47.5=\text{ 97.35}`

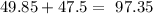
The answer is 97.35%

c)

`\begin{gathered} 100-16 \\ =84 \end{gathered}`

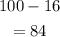
The answer is 84%