Answer:
112.8 g.
Step-by-step explanation:
What is given?
We have water vapor in the closed container:
Q (heat) = 7,500 J.
c (specific heat of water vapor) = 1.9 J/g°C.
ΔT (change of temperature) = Final temperature - Initial temperature = 140 °C - 105 °C = 35 °C.
Step-by-step solution:
To solve this problem, we have to use the formula of specific heat:
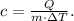
Where c is the specific heat, in this case, the specific heat of water vapor in J/g°C; m is the mass in g; and ΔT is the change of temperature in °C.
We want to find the mass of the vapor in the container, so we have to solve for 'm' and replace the given data, like this:
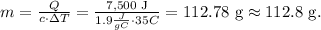
The answer would be that the mass of the vapor in the container is 112.8 g.