Question

What equation best represents the line on the given graph?

Answer 1

`\begin{gathered} \text{The equation of the line is ;} \\ y\text{ =}-2x\text{ + 4} \end{gathered}`

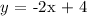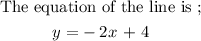
Here, we want to get the equation that best represents the line on the graph

Generally, the equation of a straight line can be represented as;

`y\text{ = mx + b}`

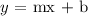
where m is the slope and b is the y-intercept

The y-intercept is the point at which the line touches the y-axis

From the graph, the point is at y = 4

So the partial equation is;

`y\text{ = mx + 4}`

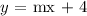
To write the full equation, we need the value of m which is the slope

To get this, we need a point on the graph

We can identify the point (2,0)

So in this case, we substitute 2 for x and 0 for y

Doing this, we have;

`\begin{gathered} 0\text{ = 2(m) + 4} \\ \\ 2m\text{ = -4} \\ \\ m\text{ = }(-4)/(2) \\ m\text{ = -2} \end{gathered}`

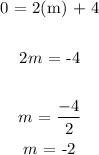
So the equation of the line is;

`y\text{ = -2x + 4}`