Question

Solve the system of equations using substitution y=3x-2y=-2x+8

Answer 1

We have the following system of equations:

`\begin{gathered} y=3x-2\ldots(A) \\ y=-2x+8\ldots(B) \end{gathered}`

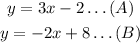
Solving by substitution method.

By substituting equation B into A, we have

`-2x+8=3x-2`

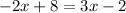
Now, by adding 2x to both sides, we get

`8=5x-2`

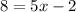
and by adding 2 to both sides, we get

`\begin{gathered} 10=5x \\ or\text{ equivalently,} \\ 5x=10 \end{gathered}`

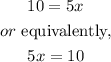
Then, by dividing both sides by 5, x is given by

`\begin{gathered} x=(10)/(5) \\ x=2 \end{gathered}`

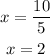
In order to find y, we can substitute this result into equation (A). It yields,

`\begin{gathered} y=3(2)-2 \\ y=6-2 \\ y=4 \end{gathered}`

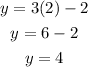
Therefore, the solution of the system is x=2 and y=4.