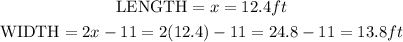Step 1. Define the length
We will call the length of the rectangle x:
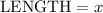
Step 2. Define the width
Since the width is 11 less than twice the length:
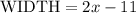
Step 3. Use the formula for the perimeter of a rectangle:
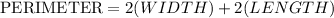
Substituting the value of the perimeter: 52.4, the width and length:
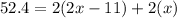
Using distributive property on the right side:
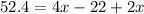
And combining like terms in the right:
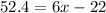
Adding 22 to both sides:
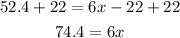
Dividing both sides by 6:
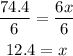
Thus, the width and length are: